Asymmetric Key Generation in Flutter

When developing applications focused on security and encryption, we may need to use Asymmetric Keys in order to encrypt and decrypt sensible data before sending it to our servers. Though the encryption algorithms may be complex, we can use the help of libraries such as Pointy Castle to integrate it in our Flutter applications.

PointyCastle is a port of Java’s Bouncy Castle and it provides us the implementation for the most commonly used cryptography algorithms. With this library we will build our example app, that will be able to create a new key pair and sign with the private key a message that we get from the user.

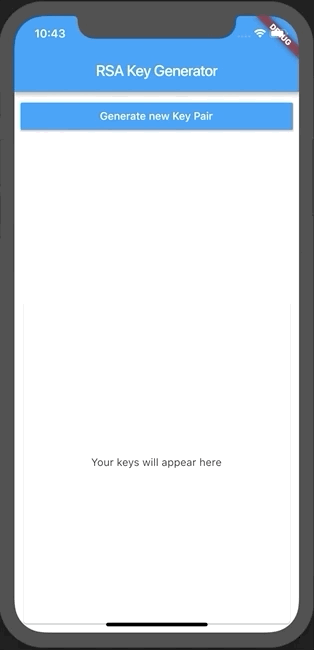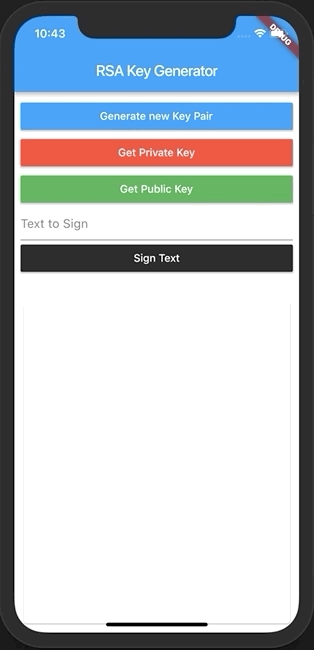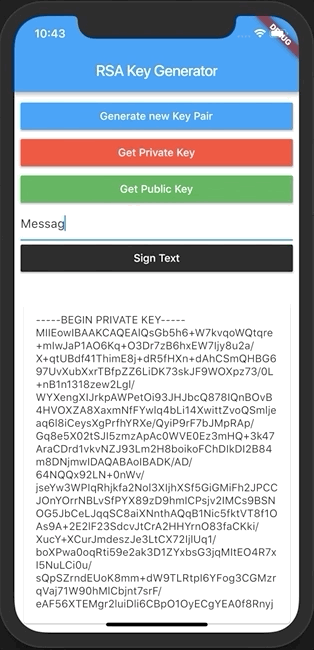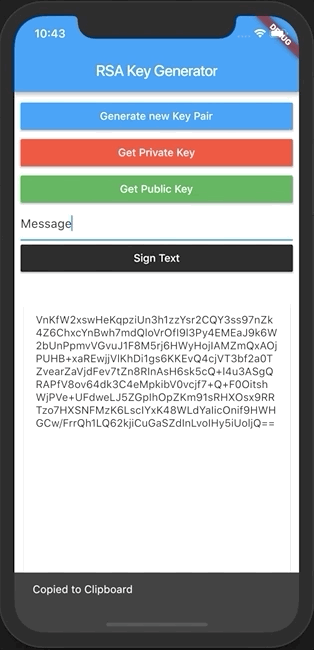
In order to achieve this result, we will have to go through the following steps:

1. Generating a RSA KeyPair using PointyCastle’s RSAKeyGenerator
2. Using Isolate for optimising the generation of a KeyPair
3. Encoding the keys PKCS1 and PKCS8 to print the keys
4. Signing a message with a Private Key
5. The curious case of generating keys in a physical iOS device in Debug Mode

Generating a RSA KeyPair using PointyCastle’s RSAKeyGenerator

RSAKeyGenerator has a convenient method called generateKeyPair() that returns a AsymmetricKeyPair<PublicKey, PrivateKey> variable which we can use to sign and verify our messages.

However, if we try to use the following code:

AsymmetricKeyPair<PublicKey, PrivateKey> createKeys() {
  var keyGenerator = new RSAKeyGenerator();
  return keyGenerator.generateKeyPair();
}

We get the error

NoSuchMethodError: The getter 'bitStrength' was called on null.
Receiver: null
Tried calling: bitStrength

Looking closely into the RSAKeyGenerator we see that the getter bitStrength is called on the variable RSAKeyGeneratorParameters _params. We can also verify that RSAKeyGenerator takes no arguments in the constructor, so the only way to set the value of _params if by using the method void init(CipherParameters params.

And this is where we jump into the rabbit hole of initialisations.

We will use the class ParametersWithRandom which extends from CipherParameters to initialise the RSAKeyGenerator.

class ParametersWithRandom<UnderlyingParameters extends CipherParameters>
    implements CipherParameters {
  final UnderlyingParameters parameters;
  final SecureRandom random;

  ParametersWithRandom(this.parameters, this.random);
}

And here we have two more objects that we need to instantiate: UnderlyingParameters and SecureRandom. For RSA Key generation, we can use RSAKeyGeneratorParameters in which we provide the bit strength, public exponent and certainty to use in the keys. On the other hand, we will need an algorithm that implements SecureRandom to satisfy the constructor. For our purposes, we will use the FortunaRandom which we will initialise shortly.

Before getting our hands into the code, we will recap what we need to do:

1. Initialise FortunaRandom and RSAKeyGeneratorParameters instances to:
2. Create a ParametersWithRandom object that is used in:
3. The initmethod of RSAKeyGenerator that we need to:
4. Create the Asymmetric KeyPair using the generateKeyPair() method.

In order to create a FortunaRandom instance, we need to give it a randomised seed of parameters which will be generated using a Random.secure(). To make our code more testable, we will wrap our code in a method:

SecureRandom getSecureRandom() {
    var secureRandom = FortunaRandom();
    var random = Random.secure();
    List<int> seeds = [];
    for (int i = 0; i < 32; i++) {
      seeds.add(random.nextInt(255));
    }
    secureRandom.seed(new KeyParameter(new Uint8List.fromList(seeds)));
    return secureRandom;
}

The RSAKeyGeneratorParameters will need 3 parameters for its initialisation, as we have discussed before:

• Public Exponent
• Certainty
• Bit Strength

For the first two parameters, we can take a look at the following Stack Overflow answer that states that the most widely used values for Public Exponent and Certainty are 65537 and 5, respectively. The Bit Strength will depend on our actual needs for the project, since a higher value will lower the performance of the code but will give us a more secure key. However, the digicert website has the following recommendation:

The Certificate Authority/Browser Forum, which created mandatory guidelines for Extended Validation (EV) certificates, has mandated a minimum key size of 2048-bits for such certificates since January 1, 2011

And with this, we can finally create our AsymmetricKeyPair<PublicKey, PrivateKey>:

SecureRandom getSecureRandom() {
    var secureRandom = FortunaRandom();
    var random = Random.secure();
    List<int> seeds = [];
    for (int i = 0; i < 32; i++) {
      seeds.add(random.nextInt(255));
    }
    secureRandom.seed(new KeyParameter(new Uint8List.fromList(seeds)));
    return secureRandom;
  }

AsymmetricKeyPair<PublicKey, PrivateKey> getRsaKeyPair(
    SecureRandom secureRandom) {
  var rsapars = new RSAKeyGeneratorParameters(BigInt.from(65537), 2048, 5);
  var params = new ParametersWithRandom(rsapars, secureRandom);
  var keyGenerator = new RSAKeyGenerator();
  keyGenerator.init(params);
  return keyGenerator.generateKeyPair();
}

But this poses a problem. Creating a key pair is an expensive operation, and in Dart we only have one “thread” of execution:

Dart code runs in a single “thread” of execution. If Dart code blocks — for example, by performing a long-running calculation or waiting for I/O — the entire program freezes.

(Asynchronous Programming: Futures | Dart)

One way we can optimise our code is by using Isolates (which you can read more in this article by Didier Bolens), which can be compared to a thread with the major difference of not being able to share memory. For convenience, Flutter has its own method to create Isolates called compute. In order to use it, we must first declare a top level function to be used as a callback and the necessary set of arguments for it. Thankfully, we can use the getRSAKeyPair function with the getSecureRandom as an argument.

Future<AsymmetricKeyPair<PublicKey, PrivateKey>> computeRSAKeyPair(
      SecureRandom secureRandom) async {
    return await compute(getRSAKeyPair, secureRandom);
  }

With this, we can finally create a pair of Asymmetric Keys using PointyCastle, but now the question is: how can we save these keys in plain text?

Encoding Asymmetric Keys to Plain Text

PEM or Privacy-Enhanced Mail, is a file format that we can use to store and send cryptography keys. Each key will have a header and a footer that indicates the type of key, as we can see in the following example.

-----BEGIN PUBLIC KEY-----
MIGfMA0GCSqGSIb3DQEBAQUAA4GNADCBiQKBgQDMYfnvWtC8Id5bPKae5yXSxQTt
+Zpul6AnnZWfI2TtIarvjHBFUtXRo96y7hoL4VWOPKGCsRqMFDkrbeUjRrx8iL91
4/srnyf6sh9c8Zk04xEOpK1ypvBz+Ks4uZObtjnnitf0NBGdjMKxveTq+VE7BWUI
yQjtQ8mbDOsiLLvh7wIDAQAB
-----END PUBLIC KEY-----

The body is composed of a Base64 String that we encode using the DER format using ASN.1. This format will tell us, for a specific encoding, what information should we retrieve from a key in order to create a structure that can be encoded to Base64. This format will depend on the type of standard that we are using for the encoding, and for this article we are using PKCS-1

Using as a reference this articleby Paul Bakker, we see that the DER structure of a Public Key using PKCS1 is:

RSAPublicKey ::= SEQUENCE {
    modulus           INTEGER,  -- n
    publicExponent    INTEGER   -- e
}

In practicality, to encode a key, we will need to create an ASN.1 structure with the modulus and publicExponent Integer. In order to create the sequence, we will first need to add to our pubspec the asn1lib package. This library gives us the tools to create a ASN1Sequence that we can populate with ASN1Integers that we can then encode.

If we look at the RSAPublicKeyand PublicKey classes, we can see that it exposes the following properties:

• e or exponent
• modulus

With this, we can start coding our DER structure:

var topLevel = new ASN1Sequence();

topLevel.add(ASN1Integer(publicKey.modulus));
topLevel.add(ASN1Integer(publicKey.exponent));

Using the encodedBytes of the ASN1Sequence we get the Uint8list to encode with base64.encode

var dataBase64 = base64.encode(topLevel.encodedBytes);

Finally, we must add the header and footer

var pemString = """-----BEGIN PUBLIC KEY-----\r\n$dataBase64\r\n-----END PUBLIC KEY-----"""

This is the resulting function:

String encodePublicKeyToPemPKCS1(RSAPublicKey publicKey) {
    var topLevel = new ASN1Sequence();

    topLevel.add(ASN1Integer(publicKey.modulus));
    topLevel.add(ASN1Integer(publicKey.exponent));

    var dataBase64 = base64.encode(topLevel.encodedBytes);
    return """-----BEGIN PUBLIC KEY-----\r\n$dataBase64\r\n-----END PUBLIC KEY-----""";
}

Next, we can follow the standard for the PrivateKey

RSAPrivateKey ::= SEQUENCE {
  version           Version,
  modulus           INTEGER,  -- n
  publicExponent    INTEGER,  -- e
  privateExponent   INTEGER,  -- d
  prime1            INTEGER,  -- p
  prime2            INTEGER,  -- q
  exponent1         INTEGER,  -- d mod (p-1)
  exponent2         INTEGER,  -- d mod (q-1)
  coefficient       INTEGER,  -- (inverse of q) mod p
  otherPrimeInfos   OtherPrimeInfos OPTIONAL
}

The RSAPrivateKey and PrivateKey object provides the following properties:

• p
• q
• exponent
• modulus
• n

The remaining properties, exponent1, exponent2 and coefficient can be calculated following the specification:

// exponent1: d mod (p-1)
var dP = privateKey.d % (privateKey.p - BigInt.from(1));

// exponent2: d mod (q-1)
var dQ = privateKey.d % (privateKey.q - BigInt.from(1));

// coefficient: (inverse of q) mod p
var iQ = privateKey.q.modInverse(privateKey.p);

This results in the following code:

String encodePrivateKeyToPemPKCS1(RSAPrivateKey privateKey) {

    var topLevel = new ASN1Sequence();

    var version = ASN1Integer(BigInt.from(0));
    var modulus = ASN1Integer(privateKey.n);
    var publicExponent = ASN1Integer(privateKey.exponent);
    var privateExponent = ASN1Integer(privateKey.d);
    var p = ASN1Integer(privateKey.p);
    var q = ASN1Integer(privateKey.q);
    var dP = privateKey.d % (privateKey.p - BigInt.from(1));
    var exp1 = ASN1Integer(dP);
    var dQ = privateKey.d % (privateKey.q - BigInt.from(1));
    var exp2 = ASN1Integer(dQ);
    var iQ = privateKey.q.modInverse(privateKey.p);
    var co = ASN1Integer(iQ);

    topLevel.add(version);
    topLevel.add(modulus);
    topLevel.add(publicExponent);
    topLevel.add(privateExponent);
    topLevel.add(p);
    topLevel.add(q);
    topLevel.add(exp1);
    topLevel.add(exp2);
    topLevel.add(co);

    var dataBase64 = base64.encode(topLevel.encodedBytes);

    return """-----BEGIN PRIVATE KEY-----\r\n$dataBase64\r\n-----END PRIVATE KEY-----""";
}

If we want to encode our keys to PKCS8, we can follow proteye’s gist: How to encode/decode RSA private/public keys to PEM format in Dart with asn1lib and pointycastle · GitHub. This gist also show us how we can decode keys from the PEM format to RSAPrivateKey and RSAPublicKey. In the RsaKeyHelper provided in the example for this article, I suggest an edit to this decode so that we can distinguish between PKCS1 and PKCS8 encoding.

Signing a message with a Private Key

Now that we have created a Private Key, we might want to sign a message with it. Fortunately for this we can use the RSASigner class provided by PointyCastle. To initialise it, we will need to state what type of digest we are going to use from the following list:

static final Map<String, String> _DIGEST_IDENTIFIER_HEXES = {
  "MD2": "06082a864886f70d0202",
  "MD4": "06082a864886f70d0204",
  "MD5": "06082a864886f70d0205",
  "RIPEMD-128": "06052b24030202",
  "RIPEMD-160": "06052b24030201",
  "RIPEMD-256": "06052b24030203",
  "SHA-1": "06052b0e03021a",
  "SHA-224": "0609608648016503040204",
  "SHA-256": "0609608648016503040201",
  "SHA-384": "0609608648016503040202",
  "SHA-512": "0609608648016503040203"
};

Using SHA-256, we will first declare a signer variable

var signer = RSASigner(SHA256Digest(), "0609608648016503040201")

Then, we need to initialise it using the RSAPrivateKey that we created before. Since we want to sign the message, the first parameter of the init method is set to true

signer.init(true, PrivateKeyParameter<RSAPrivateKey>(privateKey));

With this signer, we can use the generateSignature that returns a Uint8List . This method will require a Uint8List of the plain text we need to sign.

var signedBytes = signer.generateSignature(Uint8List.fromList(plainText.codeUnits))

Now, if we want to send this information to a backend server, we might want to encode it with base64:

var signedMessage = base64Encode(signedBytes.bytes);

With this, we have completed our sign method:

String sign(String plainText, RSAPrivateKey privateKey) {
    var signer = RSASigner(SHA256Digest(), "0609608648016503040201");
    signer.init(true, PrivateKeyParameter<RSAPrivateKey>(privateKey));
    return  base64Encode(signer.generateSignature(Uint8List.fromList(plainText.codeUnits)).bytes);
}

Using the RSAPublicKey, we could then verify this signature using the same signer with a PublicKeyParamer in its initialisation and using the verifySignature method:

bool verify(String signedMessage, String message, RSAPublicKey publicKey) {
    var signer = RSASigner(SHA256Digest(), "0609608648016503040201");
    signer.init(false, PublicKeyParameter<RSAPublicKey>(publicKey));
    message = regexMessage(message);
    return signer.verifySignature(Uint8List.fromList(message.codeUnits), RSASignature(base64Decode(signedMessage)));
}

Conclusion

And we’re finally done 🥂. We have come a long way, from creating a pair of Asymmetric Keys, to converting them to a PEM format so that they can be printed to then use the Private Key to sign the message. Though there might be easier ways to solve most of the problems depicted in this article, I hope that it may be used to show you that if you need a more custom tailored solution for your applications, you can get your hands dirty and dive into cryptography in Dart.

In the example repository you will find a fully working example of generating the keys, printing them and signing a message. As a suggestion, the next steps would involve creating a way to persist the keys and to verify signed messages while providing the PEM strings for the private and public keys.